miércoles, 4 de junio de 2014

objetivo

el objetivo de este blogger es para saber un poco mas sobre matemáticas, poner nuestros conocimientos de una forma creativa...

domingo, 1 de junio de 2014

costo marginal, mide la tasa de variación del coste dividida por la variación de la producción. Para comprender mejor el concepto de coste marginal, se suele expresar el coste marginal como el incremento que sufre el coste cuando se incrementa la producción en una unidad, es decir, el incremento del coste total que supone la producción adicional de una unidad de un determinado bien.

Matemáticamente, la función del coste marginal

CMa

es expresada como la derivada de la función del coste total

CT

con respecto a la cantidad

Q

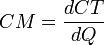
CM={\frac{dCT}{dQ}}

La curva que representa la evolución del costo marginal tiene forma de parábola cóncava, debido a la ley de los rendimientos decrecientes. En el punto mínimo de dicha curva, se encuentra el número de bienes a producir para que los costos en beneficio de la empresa sean mínimos. En dicha curva, el punto de corte con la curva de costes medios nos determina el óptimo de producción, punto a partir del cual se obtiene mayor producción.
En política de precios el coste marginal nos marca el precio a partir del cual obtenemos beneficios, siempre y cuando hayamos alcanzado el umbral de rentabilidad o punto muerto.

conclusión: costo marginal, mide la tasa de variación del coste dividida por la variación de la producción.

bibliografía: http://www.enciclopediafinanciera.com/definicion-costo-marginal.html

Extremos relativos

Si f es derivable en a, a es un extremo relativo o local si:

Si f'(a) = 0.

Si f''(a) ≠ 0.

Máximos relativos

Si f y f' son derivables en a, a es un máximo relativo si se cumple:

f'(a) = 0

f''(a) < 0

Mínimos relativos

Si f y f' son derivables en a, a es un mínimo relativo si se cumple:

f'(a) = 0

f''(a) > 0

bibliografía: http://www.vitutor.com/fun/5/c_9.HTML

conclusión:

Máximo absoluto

Una función tiene su máximo absoluto en el x = a si la ordenada es mayor o igual que en cualquier otro punto del dominio de la función.

Mínimo absoluto

Una función tiene su mínimo absoluto en el x = b si la ordenada es menor o igual que en cualquier otro punto del dominio de la función.

Derivadas de orden superior

es una función diferenciable, es posible considerar su función derivada como:

$f'=\{(x,y)/\;y=D_{x}f(x)\}$ para

en el dominio

.
Si para algunos valores $x \in M$ existe el $\displaystyle{\lim_{h \rightarrow{0}}{\frac{f'(x+h)-f'(x)}{h}}}$ se dice que existe la segunda derivada de la función

que se denota por

o $D_{x}^{2}f(x)$ , que equivale a $D_{x}[D_{x}f(x)]$ . O sea, la segunda derivada de la función

se obtiene derivando la primera derivada de la función.

bibliografía:http://www.tec-digital.itcr.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/node11.html