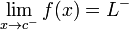Matematicas: mayo 2014

sábado, 31 de mayo de 2014

La regla de la cadena y la regla de la potencia

La regla de la cadena Si u es una función diferenciable de x, y f es una función diferenciable de u, entonces f es una función diferenciable de x, y:

[f(u)]

f'(u)

Ejemplo Tomando f(x) = x³, obtenemos

u³

3u²

En palabras:

La derivada de una cantidad al cubo es igual a 3 veces la cantidad (original) al cuadrado por la derivada de la cantidad.

A veces se refiere a esto como un ejemplo de la regla generalizada de las potencias. Más ejemplos

(1+x²)³

3(1+x²)²

(1+x²)

La derivada de una cantidad al cubo es 3 veces la cantidad (original) al cuadrado por la derivada de la cantidad.

3(1+x²)²^,2x

6x(1+x²)²

(x+x²)³

2(x+x²)^-3

2(-3)(x+x²)^-4

(x+x²)

La derivada de una cantidad elevada a la -3 es -3 veces la cantidad (original) elevada a la -4 por la derivada de la cantidad.

-6(x+x²)^-4

(1+2x)

-6(1+2x)

(x+x²)⁴ http://www.zweigmedia.com/MundoReal/tutorials/frames3_2.html

jueves, 29 de mayo de 2014

reglas de derivacion

Derivada de una constante por una función

H) f es derivable en x=a
T) (kf(a))' = k.f'(a)

Demostración:

                                              f'(a)
                                         ------^------    
                 k.f(x) - k.f(a)         (f(x) - f(a))
(k.f(a))' = lim ---------------- = lim k ------------- = k.f'(a)
            x->a      x - a        x->a      x - a

Nota:

El teorema anterior da el valor de la derivada en el punto a. Como a es un punto genérico, lo sustituimos por x y tenemos la función derivada:
(kf)'(x) = k.f'(x), si f es derivable en x.

Derivada de la suma

La derivada de una suma de funciones es la suma de las derivadas de cada función.

H) f es derivable en x=a, g es derivable en x=a
T) f+g es derivable en x=a
(f+g)'(a) = f'(a) + g'(a)

Demostración:

                (f+g)(x) - (f+g)(a)       f(x) + g(x) - f(a) - g(a)
(f+g)'(a) = lim ------------------- = lim -------------------------
            x->a      (x-a)           x->a         (x-a)
   
                f(x) - f(a)    g(x) - g(a)
          = lim ----------- + ------------ = f'(a) + g'(a)
            x->a   (x-a)          (x-a)

Notas:

En general (f+g)'(x) = f'(x) + g'(x), si f y g son derivables en x.
El teorema se extiende a más de dos funciones.

Derivada del producto

H) f es derivable en x=a, g es derivable en x=a
T) f.g es derivable en x=a
(f.g)'(a) = f'(a).g(a) + f(a).g'(a)

Demostración:

                (f.g)(x) - (f.g)(a)       f(x).g(x) - f(a).g(a)
(f.g)'(a) = lim ------------------- = lim --------------------
            x->a      (x-a)           x->a       (x-a)

      f(x).g(x) - f(a)g(a) + f(a)g(x) - f(a)g(x)
= lim ------------------------------------------ =
  x->a                 (x-a)

             f'(a)               g'(a)
(*) g(a) -----^-----         -----^-----
    -^- (f(x) - f(a))       (g(x) - g(a))
lim g(x)------------- + f(a)------------- = f'(a).g(a) + g'(a).f(a)
x->a        (x-a)               (x-a)

(*) Pues g es derivable en a => (teorema) g es continua en a
=> (def. de continuidad) existe g(a) y lim_x->ag(x)=g(a).
Notas:

(f.g)'(x) = f'(x).g(x) + f(x).g'(x).
Generalización para tres funciones: (f(x).g(x).h(x))' = f'(x).g(x).h(x) + f(x).g'(x).h(x) + f(x)g(x).h'(x)

Derivada del cociente

H) f es derivable en x=a, g es derivable en x=a, g(a) distinto de 0
T) f/g es derivable en x=a
(f/g)'(a) = (f'(a).g(a) - f(a).g'(a))/g²(a)

Demostración:

                (f/g)(x) - (f/g)(a)       f(x)/g(x) - f(a)/g(a)
(f/g)'(a) = lim ------------------- = lim ---------------------
            x->a       x - a          x->a        x - a

      f(x)g(a) - g(x)f(a) + f(a)g(a) - f(a)g(a)
= lim ----------------------------------------- =
  x->a             (x - a)g(x)g(a)

             f'(a)               g'(a)
         -----^-----         -----^-----
        (f(x) - f(a))       (g(x) - g(a))
    g(a)------------- -  f(a)-------------    g(a)f'(a) - f(a)g'(a)
lim         x - a               x - a       = --------------------
x->a ------------------------------------          g²(a)
              g(x)g(a)
               '--> g(a) (*)

(*) Pues g es derivable en a => (teorema) g es continua en a
=> (def. de continuidad) existe g(a) y lim_x->ag(x)=g(a).
Nota:

(f/g)'(x) = (f'(x)g(x) - f(x)g'(x))/g²(x).

Derivada de la función compuesta

Regla de la cadena

H) f es derivable en x=a, g es derivable en x=f(a)
T) gof es derivable en x=a
(gof)'(a) = g'[f(a)].f'(a)

Demostración:

                               g[f(x)] - g[f(a)]
(gof)'(a) = [g[f(x)]'(a) = lim ----------------- =
                           x->a     x - a

            g'[f(a)]        f'(a)
     --------^--------  ----^----
     g[f(x)] - g[f(a)]   f(x) - f(a)
lim ------------------ . ---------- = g'[f(a)].f'(a)
x->a   f(x) - f(a)         x - a

Nota:

(gof)'(x) = g'[f(x)].f'(x).

bibliografía:http://matematica.50webs.com/reglas-de-derivacion.html

Diferenciabilidad y continuidad

Derivada; Diferenciabilidad
La derivada de una función f en el punto a en su dominio se define por

f'(a)

lim
h

f(a+h) - f(a)

Decimos que la función f es diferenciable en el punto a en su dominio si f'(a) existe. Diferenciable en un subconjunto del dominio
La función f es diferenciable en el subconjunto S de su dominio si es diferenciable en cada punto de S. Nota

Una función puede fallar ser diferenciable en el punto a si

lim
h

f(a+h) - f(a)

no existe, o es infinito.

En el primer caso, a veces tenemos una cúspide en la gráfica, y en el último caso, obtenemos un punto de tangencia vertical.

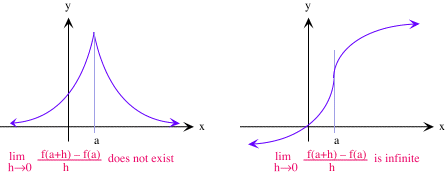
bibliografía:http://www.zweigmedia.com/MundoReal/calctopic1/contanddiffb.html

Derivada como razón de cambio

Diferenciación de funciones por incrementos

Este tipo de derivadas no cuenta con una formula especifica. Las reglas que se tienen que seguir para poder solucionar las derivadas por incremento es de la siguiente manera. De la formula inicial se le agrega en el conjunto que tiene la variable,Delta "x" o Incremento simbolizado . Despues de la formula que tiene se le resta la formula original. posteriormente se soluciona como un limite dividiendo el resultado entre y de esta manera se soluciona una derivada por incremento.

Bibliografía: http://www.angelfire.com/planet/reivaj7890/derivadas_por_incremento.htm

Derivada de una función

La función derivada de una función f(x) es una función que asocia a cada número real su derivada, si existe. Se expresa por f'(x).

Ejemplos

Determinar la función derivada de f(x) = x² − x + 1.

conclusión: la derivada de una función es la que cambia el valor de dicha función matemática.

interes compuesto

El interés compuesto representa la acumulación de intereses devengados por un capital inicial (C_I) o principal a una tasa de interés (r) durante (n) periodos de imposición de modo que los intereses que se obtienen al final de cada período de inversión no se retiran sino que se reinvierten o añaden al capital inicial, es decir, se capitalizan.

conclusión: Capital final (C_f) = capital inicial (C) más los intereses.

bibliografía:http://www.profesorenlinea.cl/matematica/Interes_compuesto.html

Continuidad y discontinuidad

Continuidad:

Se dice que una función f(x) es continua en un punto x = a si y sólo si se cumplen las tres condiciones siguientes:

1. Que el punto x = a tenga imagen.

2. Que exista el límite de la función en el punto x = a.

3. Que la imagen del punto coincida con el límite de la función en el punto.

Discontinuidad:

Una función es discontinua en un punto, x = a, si:

1.El punto, x = a, no tiene imagen.

La función es discontinua en x = 2 porque no existe imagen.

2. Que no exista el límite de la función en el punto x = a.

La función es discontinua en x = 2 porque no tiene límite.

3. Que la imagen del punto no coincida con el límite de la función en el punto.

La función es discontinua porque en x = 2 no coincide la imagen con el límite.

miércoles, 21 de mayo de 2014

Límites infinitos - Infinite limits

limite al infinito

Decimos que lim f(x)= $\infty$ si para los valores de x proximos a a, x→ a los valores de f(x) pueden hacerse tan grandes como queramos.

Con rigor, decimos que lim f(x)= $\infty$ si fijado a un valor k positivo y tan grande como se quisiera, existe un entorno de a, E(a, ∂), tal que si x ∈ E (a,∂ ) y x ≠ a, entoces f(x)>k.

Análogamente, lim f(x) = - $\infty$
x→a

si para los valores de x cercanos a a, los valores de f(x) se pueden hacer tan pequeños como queramos.

Diremos que lim f(x) = - $\infty$
x→a

si fijado un valor de k positivo y tan grande como se quisiera, podemos encontrar un entorno de a, E(a, ∂), tal que si x ∈ E (a,∂ ) y x ≠ a, entonces f(x) < -k

•Ejemplo:

la función f(x)= 1/|x|

En el punto x=0 se tiene:

lim 1/|x| = - $\infty$
x→ 0-
→ lim 1/|x| = $\infty$ x→0

lim 1/|x| = $\infty$
x→a’

limites laterales

De manera similar, x puede aproximarse a c tomando valores más grandes que éste (derecha):

\lim_{x \to c^+}f(x) = L^+

o tomando valores más pequeños (izquierda), en cuyo caso los límites pueden ser escritos como:

\lim_{x \to c^-}f(x) = L^-

Si los dos límites anteriores son iguales:

\lim_{x \to c^-}f(x) = \lim_{x \to c^+}f(x) = L

entonces L se pueden referir como el límite de f(x) en c. Dicho de otro modo, si estos no son iguales a L entonces el límite, como tal, no existe.