tipos de funciones

Función polinómica: aquellas funciones cuya expresión algebraíca es un polinomio, es decir, las funciones polinómicas, tienen como dominio todo el conjunto de los números reales.

 

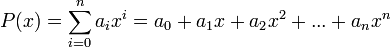
 Función racional: para calcular el dominio de este tipo de funciones el primer paso es igualar el denominador a cero y resolver esa ecuación, una vez ya resuelta esa ecuación el dominio estara formado por todos los reales excepto las soluciones de la ecuación.

 

Función irracional: son las que vienen expresadas atravez de un radical que lleve radicando la variable independiente. Si el radical tiene número impar, entonces el dominio sera todo el conjunto R de los números reales porque al elegir cualquier valor de X siempre vamos a poder calcular la raiz de indice impar de la expresión que haya en el radicando. Pero si el radical tiene indice par, para los valores de X  que hagan el radicando negativo no existira la raiz y por tanto no tendra. 

Función exponencial: tienen como rango todos los números reales positivos sin incluir el cero. 

Función logarítmica:  los números negativos y 0 no existen y deben ser mayores a cero.

Para calcular su dominio es bastante similar al de las funciones irracionales. Tomando lo que hay dentro del logaritmo y hacemos que sea mayor que cero. 

El rango estara representando por el conjunto de todos los números reales.

Conclusión:

Función polinómica: tiene como dominio todo los números reales.

Función racional: es el cociente de dos funciones polinómiales.

Función exponencial: es cuando la variable esta en el exponente.

Función entera: es la que pertenece constante independiente misma de su constante.