Derivada; Diferenciabilidad La
derivada de una función f en el punto a en su dominio se define por
| f'(a) | = | lim
h 0 |
f(a+h) - f(a)
h
|
Decimos que la función f es
diferenciable en el punto a en su dominio si f
'(a) existe.
Diferenciable en un subconjunto del dominio La función f es
diferenciable en el subconjunto S de su dominio si es diferenciable en cada punto de S.
Nota
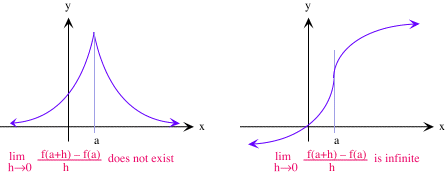
| Una función puede fallar ser diferenciable en el punto a si | lim
h0 |
f(a+h) - f(a)
h
| no existe, o es infinito. |
En el primer caso, a veces tenemos una cúspide en la gráfica, y en el último caso, obtenemos un punto de tangencia vertical.
bibliografía:http://www.zweigmedia.com/MundoReal/calctopic1/contanddiffb.html
No hay comentarios:
Publicar un comentario