En matemáticas, el logaritmo de un número —en una base de logaritmo determinada— es el exponente al cual hay que elevar la base para obtener dicho número. Por ejemplo, el logaritmo de 1000 en base 10 es 3, porque 1000 es igual a 10 a la potencia 3: 1000 = 103 = 10×10×10.
Para representar la operación de logaritmo en una determinada base se escribe la abreviatura log y como subíndice la base y después el número resultante del que deseamos hallar el logaritmo. Por ejemplo, 35=243 luego log3243=5. Cuando se sobreentiende la base, se puede omitir.
Los logaritmos mantienen ciertas identidades aritméticas muy útiles a la hora de realizar cálculos:
- El logaritmo de un producto es igual a la suma de los logaritmos de los factores.
- El logaritmo de un cociente es igual al logaritmo del numerador menos el logaritmo del denominador.
- El logaritmo de una potencia es igual al producto entre el exponente y el logaritmo de la base de la potencia.
- El logaritmo de una raíz es igual al producto entre la inversa del índice y el logaritmo del radicando.
En realidad la tercera y cuarta identidad son equivalentes, sin más que hacer:
- El logaritmo de a en la base b es igual al cociente del logaritmo de a en la base c, entre el logaritmo de b en la base c.3
- Sea l el logaritmo de a en la base b, entonces el logaritmo de la potencia emésima de a en la base b a la n es lm/n4
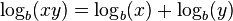
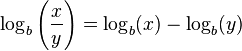
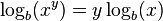
![\!\, \log_b(\sqrt[y]{x}) = \frac{\log_b(x)}{y} \,](http://upload.wikimedia.org/math/e/3/2/e32fd943d2fc67a7033c9d67046522e3.png)
![\!\, \sqrt[y]{x} = x^\frac{1}{y} \,](http://upload.wikimedia.org/math/e/7/d/e7d30a4c68d2e42f12b4fd6bc4417864.png)
hola.... Cintia buen trabajo
ResponderEliminar